O que é uma função ?

Uma função é uma relação especial, que é definida da seguinte maneira: sejam dois conjuntos A e B, tais que para todo elemento x pertencente a A, haja uma correspondência de um elemento y pertencente a B. Essa correspondência é a função: a associação, definida de algum modo, entre todos os elementos de um conjunto e os elementos de outro conjunto.

A função que associa um elemento x a outro valor pode ser indicada por f(x). O aparecimento de x na simbologia da função não ocorre por acaso, uma vez que o valor f(x) depende de x. Por isso mesmo, x é chamada variável independente e f(x) (ou y) é chamada de variável dependente. Matematicamente a função é definida:

, ou mais simplificadamente,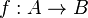 

Um exemplo de função: dado o conjunto dos números naturais, uma função pode associar cada número ao seu quadrado. Assim, essa função assumiria os valores: { 1,4,9,16,... }.

Uma função pode, na verdade, associar mais de um conjunto a outro; podem haver diversas variáveis independentes. Por exemplo: uma função pode tomar dois valores inteiros e expressar sua soma:

No entanto, neste livro será dada mais atenção às funções de uma variável, apenas. São duas características da função enquanto relação:

• há correspondência unívoca entre um elemento e o valor associado a ele pela função: isso significa que para cada valor assumido pela variável independente (x), há um único valor da variável dependente (y) associado pela função. Consequentemente, se t = f(x) e w = f(x), então t = w.
• a correspondência é total, ou seja, um valor assumido pela variável dependente estará associado para todo valor possível de ser assumido pela variável independente.

A tabela a seguir mostra dois exemplos de relações que não são funções:

Nesse caso, um mesmo elemento (3) do domínio X aparece associado a dois elementos do contradomínio Y (c,d).	Aqui a correspondência não é total: falta um valor associado a 1.

Já o diagrama a seguir representa uma função:

Duas funções f(x) e g(x) são ditas iguais (f = g) se e somente se para cada valor de x no domínio D, f(x) e g(x) assumam o mesmo valor:

Relações que estabeleçam dependência entre os elementos de dois conjuntos são denominadas funções.

Um exemplo clássico de função é a do salário de vendedores que ganham por comissão:

Existe um valor fixo que o vendedor ganha mesmo se não conseguir vender nada naquele mês e uma comissão, que depende da quantidade de vendas que o vendedor realizou. Por exemplo:

Gráfico salário X vendas

Vendas	Comissão por venda	Valor Fixo	Salário
0	55	300	300
1	55	300	355
2	55	300	410
...	...	...	...

Da tabela acima podemos construir uma relação entre as vendas e o salário do vendedor:

E com isso, construímos um gráfico que relaciona vendas a salário, onde verifica-se que:

• O salário depende das vendas.
• O salário é uma função das vendas.

Ao aplicar uma função 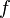 em um dado conjunto , cada elemento deste deverá ter como correspondente um elemento em um dado conjunto .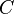

Ao conjunto  denomina-se domínio da função, sendo seus elementos denominados abcissas, e ao conjunto 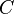 denomina-se contra-domínio, sendo seus elementos denominados ordenadas ou imagens, quando estas se correlacionarem a um elemento de .

Ou seja:

Dados dois conjuntos  e 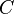 não vazios, dizemos que a relação f de  em 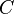 será função se, e somente se,

.

(Para qualquer x pertencente a D existe um y pertencente a C tal que o par ordenado (x,y) pertence à função f)

Obs : Para cada , deve haver apenas um 

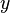
Existem várias maneiras de se representar funções.

Abaixo você pode ver as três mais comummente utilizadas, sendo a primeira a predominante.

As representações abaixo são de uma função em relação a seu domínio e contra-domínio.

Há também as representações por sua fórmula algébrica em relação a sua imagem, como a seguir:

.

As condições básicas de existência são:

1. Todo e qualquer elemento do domínio deve possuir uma única imagem no contra-Domínio.
2. Caso a equação algébrica da função contenha uma fracção, seu denominador deve ser diferente a 0 (zero).
3. Caso a equação algébrica da função possua uma raiz de índice par, para que seu resultado pertença aos Reais, o radicando deve ser maior ou igual a 0 (zero).
   1. Caso essa mesma raiz esteja no denominador de uma fracção, o radicando deve ser estritamente maior que 0 (zero).
   2. Caso o índice dessa raiz seja um número ímpar, a única restrição é que o radicando seja diferente de 0 (zero).

Com isso, cada função deverá ter suas restrições particulares, mas sempre obedecendo as gerais acima. Algumas regras não são aplicáveis a funções com contradomínio Complexo.

Domínio, contradomínio e imagem:

Função x², definida para { -3,-2,-1,0 }. Observar o conjunto domínio (D), contra-domínio (CD) e imagem (delineado pela linha tracejada).

São três conjuntos especiais associados à função. O domínio é o conjunto A do exemplo dado no início deste capítulo: contém todos os elementos x para os quais a função deve ser definida. Já o conjunto B do exemplo é o contradomínio: o conjunto que contém os elementos que podem ser relacionados a elementos do domínio.

Também define-se o conjunto imagem como o conjunto de valores que efectivamente f(x) assume. O conjunto imagem é, pois, sempre um subconjunto do contradomínio.

Por exemplo, suponha a função que associa um elemento do domínio D = { 1,2,3,4,5 } a uma vogal ordenada no alfabeto.

O domínio, já especificado, é 

O contradomínio é 

A imagem é 

Gráfico Cartesiano

Abcissa 

Todo e qualquer elemento do domínio.

Ordenada 

Todo e qualquer elemento do conjunto imagem.

Gráfico em Plano Cartesiano da função 

Representação de todos os pontos que compõem uma função através de dois eixos perpendiculares.